Mesopotamia civilization
Mesopotamia civilization is the civilization which was found between rivers Tilgris and Euphrates now present in countries like Turkey, Syria along with major part of Iraq having following civilizations,
- Sumerian civilization: They were present between the period 3500 BC – 2400 BC (appox.) and later invaded by Babylonians
- Babylonians: They were present from 2000 BC to 550 BC.
Most of the mathematical work found was between the period 2500 – 1600 BC.
Facts
- Cuneiform Scripts: Sumerians were using form of writting which was based on cuneiform (i.e. wedge-shaped) symbols. They wrote symbols/alphabets/numerals on wet clay tablets and were allowed to get baked in the hot sun or fire. Many such tablets, not all, have survived today. They had a proper civilization with schools and it is believed that Babylonians students had written most of the tablets as exercises or in class rooms and made an effort to preserve them for references. Various topics the tablets covered are algebra, quadratic equations,fractions, cubic equations, square roots, Pythagorus Triples, geometry but scientists found that they were not very correct in geometry.
- Babylonian Mathematics:
- Sumerians and Babylonians used sexagesimal number system i.e. they followed Base 60 pattern (We follow decimal pattern | Base 10) and thay had NO ZERO concept.
- It is believed that they followed base 60 pattern as 60 is a number which has wide range of factors like 1,2,3,4,5,6,10,12,15,20,30 and 60.
- They used 2 wedges(“) to represent 0.
Eg: 106 were written as 1”6 or 1 6.
But no wedges were found if the last digit was 0.
Eg: 16 would be written as 16 and 160 would be written as 16 as well. No differentiation was present between them. - Babylonians probably didn’t knew the circle has 360 degrees but they successfully subdivided the circle in 360 parts by using the angle of an equilateral triangle as the basic unit and further subdivided into 60 more parts following their sexagesimal numeric system.
- Babylonians divided a day into 24 hours, hour into 60 minutes, minute into 60 seconds. We follow same today. To write 5h 25′ 30″, i.e. 4 hours, 15 minutes, 10 seconds,they used to write in sexagesimal fraction as 4 15/60 10/3600. We adopt the notation 4; 15, 10 for this sexagesimal number.
- They had prepared tablets of squares and cubes and they used this tablet in multiplication of numbers. Also, they had prepared tablet for reciprocal of numbers and used it while carrying out division of numbers.
- Numerals and Mathematics:
# Numerals from 1 to 59:
For Numerals greater than 59, they used place system method:
3 4 =3X60 + 4= 184 (Note the space between 3 and 4)
1 26 = 1×60 + 26 = 86
4 43 56 = 4×602 + 43×60 + 56.
We would have written in decimal format as 4×102 + 43×10 + 56
Decimals:
10,23,54;32,54= 10×602 + 23×60 + 54 + 32/60 + 54/602.
We would have written in decimal format as 10×102 + 23×10 + 54 + 32/10 + 54/102.
# Many separate tablets were found having product of numbers equal to 60, tables of 5 (tablet NBC7344 ), 12-times table (tablet MS2184/3), 10-times table (tablet VAT7858) and many such tables
# Multipication: To carry out multiplication seperate tablets were prepared with squares of numbers up to 59 and the cubes of numbers up to 32.
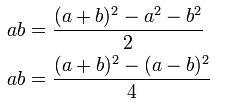
# Division: They also had prepared tablets consisting of reciprocals of many numbers.
Of several table one of the table they prepared is
| 2 | 0; 30 |
| 3 | 0; 20 |
| 4 | 0; 15 |
| 5 | 0; 12 |
| 6 | 0; 10 |
| 8 | 0; 7, 30 |
| 9 | 0; 6, 40 |
| 10 | 0; 6 |
| 12 | 0; 5 |
| 15 | 0; 4 |
| 16 | 0; 3, 45 |
| 18 | 0; 3, 20 |
| 20 | 0; 3 |
| 24 | 0; 2, 30 |
| 25 | 0; 2, 24 |
| 27 | 0; 2, 13, 20 |
For calculating ‘a/b’ they followed the concept of a x 1/b.
From the reciprocal tables they prepared they used to find 1/b and then multiply it by a to get a/b.
If observed carefully they didnt calculate reciprocals of prime numbers except 2, 3 and 5(prob because 60 is divisible by only these prime numbers). For reciprocals of other prime numbers they used to follow technique of proportion and approximation. They would write 1/13 = 7/91 = 7 x (1/91) =(approx.) 7.(1/90) and these values were obtained from the tables.
# Quadratic Equations:
To solve a quadratic equation x2 + bx = c
They used the formula:
x = -b/2 + v[(b/2)2+ c]
And for obtaining square root they used to check the same squares table in reverse way.
# Cubic Equations:
They also had prepared table for n3+n2 and used this table for solving cubic equations of following type
ax3 + bx2 = c
Multiplying the equation by a2 and dividing by b3 gives
(ax/b)3 + (ax/b)2 = ca2/b3
Substituting y = ax/b gives
y3 + y2 = ca2/b3
Now they used to check the table to get the closest value to RHS and corresponding value of n would be equal to y. From y they used to calculate x.
# Pythagorus Triples:
One of the tablets showed that they had some knowledge of the pythagorus theorem (arnd 1500 years before Pythagorus was born).
Tablet Plimpton 322 has been found which has the Pythagorus Triples.
Tablets
-
Plimpton 322 Tablet:
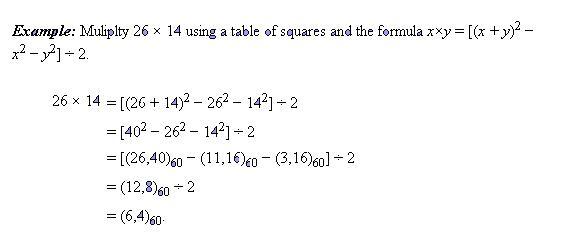
-
Yale Tablet:
Tablet has a process to calculate sqrt of 2 using Pythagorus Theorem.

Yale Tablet has a diagram of a square with 30 on one side, the diagonals are drawn in and near the centre is written 1,24,51,10 and 42,25,35 (sexagesimal format). Assuming that the first number is 1; 24,51,10 then converting this to a decimal gives 1.414212963 while v2 = 1.414213562. Calculating 30 × [ 1;24,51,10 ] gives 42;25,35 which is the second number. The diagonal of a square of side 30 is found by multiplying 30 by the approximation to v2. (45-45-90 triangle).
-
Susa Tablet
The Susa tablet sets out a problem about an isosceles triangle with sides 50, 50 and 60. The problem is to find the radius of the circle through the three vertices (Image: Replica of Susa Tablet)
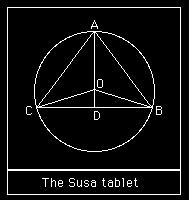
Here we have labelled the triangle A, B, C and the centre of the circle is O. The perpendicular AD is drawn from A to meet the side BC. Now the triangle ABD is a right angled triangle so, using Pythagorus theorem AD2 = AB2 – BD2, so AD = 40. -
Yale YBC Tablet
Babylonians used the value of pi as 3.This was found from the tablet Yale YBC

- Here the 3 = circumference of circle
9 is the square of 3.
45 is the Area of the circle.Circumference of circle: 3 = 2pr. So r2 = 9/(4 p2)
Area of circle: A=pr^2 = 9/(4p) = 9/(4×3) = 9 x 0;05 = 0;45

Leave a Reply
You must be logged in to post a comment.