Shorcuts for Division in Vedic Mathematics

 

Like Multiplication, Tirthaji Maharaj has classified tricks to Divide Numbers in Vedic Mathematics in Specific and General Methods. Specific Division Methods can be applied when numbers satisfy certain conditions like Divisor slightly less than 100 or Divisor slightly greater than power of 10 or Divisor is ending with 9, etc. While General Multiplication Methods can be applied to any types of numbers.

Depending of Divisor and Dividend, Division in Vedic Mathematics are classified in the form of Sutras as below. Lets see the Vedic Mathematics Division techniques:

1. Nikhilam Sutra (Specific Technique)
2. Paravartya Sutra (Specific Technique)
3. Anurupyena Sutra (Specific Technique)
4. Direct Flag Method (General Technique)
5. Ekadhikena Purvena (Specific Technique)
6. Vestanas (General Technique)

Nikhilam Sutra:

Nihilam Sutra is a Specific Method to Divide Numbers using Vedic Mathematics. This Vedic Maths Division Method can be applied when Divisor is closer to power of 10 BUT less than that of it.

Using Nikhilam Sutra, you can easily divide when divisor is like 98, 92, 995, 89997, etc.

Lets see division math tricks using Nikhilam Sutra. Example: 243/9

Process: 

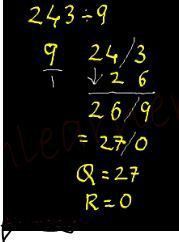
1. 9 is 1(deficiency) less than 10(nearest power of 10). (that 1 is written in white color below divisor in example)
2. Split Dividend in 2 parts (Quotient & Remainder) in such a way Remainder to have same number of digits as that of Divisor. In this case its 1 digit.
3. Take 1st digit – 2 down as it is.
4. Multiply the above deficiency (1) with the 2 and put below 4 and add them column wise to get 6.
5. Multiply deficiency (1) by 6 and put below 3 and add column wise to get 9.
6. As last column is filled, we stop the process.
7. We know the concept that Remainder can NEVER be >= Divisor, as Remainder 9 is = our Divisor 9, we divide 9 by 9 to get Quotient 1 and Remainder as 0.
8. Add the Quotient 1 to original Quotient 26 to get 27.
9. Thus Quotient=27 & Remainder=0.

 

Click Here => To Check More Examples on Vedic Maths Tricks for Division using Nikhilam Sutra.

Paravartya Sutra:

This is another Shortcut Method of Division in Vedic Mathematics. 

Paravartya Sutra is a Specific Method for division in Vedic Maths. This Vedic Maths Division Method can be applied when Divisor is closer to power of 10 BUT greater than that of it.

Using Paravartya Sutra, you can easily divide when divisor is like 123, 104, 1112, etc.

Lets see division math tricks using Nikhilam Sutra. Example: 432/11

 

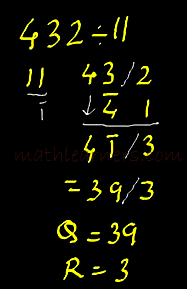
# 432/11

• Discard the 1st digit(1) of Divisor(11) and take Transpose of remaining digits(i.e. -1 or Bar 1).
• Split Dividend in 2 parts (Quotient & Remainder) in such a way that Remainder part should have same number of digits thus obtained in 1st step.Thus remainder part will have only 1 digit
• Now carry the same process as done with previous (Nikhilam) method.
• If any bar digit is present in final answer, convert to Normal method using Vinculum.

 

Click Here => To check more examples of vedic division tricks using Paravartya Sutra.

 

Anurupyena Sutra

Anurupyena Sutra is another Specific Vedic Maths Division Tricks which shows how to divide numbers when Nikhilam and Paravartya are not applicable.

Using Anurupyena Sutra, we multiply Divisor by a factor so that either Nikhilam or Paravartya Sutra can be applied.

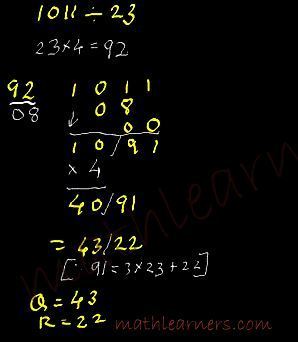
Example: 1011/23

• Divisor is 23. Multiply by factor(4) to get 92 so that Nikhilam Sutra of Division can be applied.
• As per Nikhilam Sutra, 92 is 8 less than 100 (base). Hence write 08 under 92 (Base is 100 so we need 2 digits)
• Apply Nikhilam Sutra as discussed previously.
• As per Anurupyena Sutra, multiply the Quotient by the factor used earlier i.e.4.
• As we know the concept that Remainder can NEVER be >= Divisor, as Remainder 91 is greater than our Divisor 23, we divide 91 by 23 to get Quotient 3 and Remainder as 22.
• Add this Quotient 3 to original Quotient 40 to 43 as new Quotient.
• Thus Final Answer, Quotient = 43 and Remainder = 22.

Click here => Check Process and More Examples Vedic Maths Tricks of Anurupyena Sutra.

Vinculum Process of Division

Vinculum is another division in vedic maths tricks which can be applied when Divisor has digits greater than 5.

Using Vinculum Process, convert those bigger digits to smaller digit and then apply Nikhilam Sutra or Paravartya Sutras of Division.

Example:

 

Click Here => Check More Examples on Division in Vedic Maths using Vinculum Process.

Direct Flag Division:

Direct Division (Flag Method) is a general method of Division in Vedic Mathematics shows shortcut to divide any types of numbers. It is a  shortcut method for division of large numbers.

Single Digit Flag

1234/12 – Dividend = 1234 and Divisor = 12. Split divisor (12) in 2 parts (1 and 2) where division will be carried using ONLY 1(new divisor) and 2 is called as flag. As flag is single digit, Split dividend in 2 parts such that 2nd part will have same number as that of flag i.e. 1 digit.

Process (see the example for each step):

1. Division of 1 by 1 (Q=1 and R= 0). Write Q=1 and carry forward the R=0(written in white under and between 1&2).
2. Multiply the new Q(1) with the flag(2) and subtract this product from 02 = 0 and divide this subtraction by 1. It gives Q= 0 and R= 0(Carry forward R=0). (i.e. Multiply, Subtract, Divide)
3. Follow same above process, So multiply new Q(0) with flag(2) and subtract this product from 03 = 3 and divide this subtraction by 1. It gives Q= 3 and R= 0(Carry forward R=0).
4. For remainder we carry same process EXCEPT we don’t divide. (i.e. Multiply, Subtract) So multiply new Q(3) with flag(2) and subtract this product from 04 = -2. As we get negative subtraction, we reduce the quotient by 1 and increase the remainder by the 1st multiplier of new multiplier (1X1 =1). So new Q = 2 and new R =1. (Refer Topic Work with Quotient and Remainder). We carry this method till we don’t have negative subtraction.
5. Now Multiply the new Q(2) with the flag(2) and subtract this product from 14 = 10(positive) and put it down as it is.
6. So final answer: Quotient = 102 and Remainder = 10 (Remainder should always < Divisor| (Refer Topic Work with Quotient and Remainder).

Click Here => Check the process and more examples of Direct Flag Method of Vedic Maths.

Ekadhikena Purvena

It is another shortcut method of division in Vedic Maths when Divisor is ending with 9.

Example 1/19:

For the denominator 19, the purva (previous) is 1.
Hence Ekadhikena purva (one more than the previous) is 1 + 1 = 2.
Now, As per Ekadhikena Purvena, we will be using 2 for Division purpose.

Steps:

• Divide 1 by 2 which gives Quotient as 0(written with yellow) and Remainder as 1 (written on left side of Quotient with White)
• Now divide 10 by 2 which gives Quotient as 5(written with yellow) and Remainder as 0 (written on left side of Quotient with White)
• Now divide 05 by 2 which gives Quotient as 2(written with yellow) and Remainder as 1 (written on left side of Quotient with White)
• Similarly go on carrying this process till you find same pair of Quotient and Remainder is obtained.
• At the end we get 01, on dividing it by 2 we get Quotient as 0 and Remainder as 1. So that means same series (from blue dot to blue dot) will keep on repeating.
• So the series written in yellow color is final answer.

Ekadhikena Purvena can be applied to divisors ending with 8,7, 1,2,3 .

Click Here => To check More Examples of Ekadhiekna Purvena

Vestanas

Vestanas also called as Osculators is General Method in Vedic Mathematics, which is used to find a number is exactly divisible by the mentioned divisor.

Click Here => To understand the process and examples of Vestanas.

 

If you like this post please share on Facebook, Google+, Twitter, etc.