mathlearners

You are here: Home / What is Vedic Mathematics / Shorcuts for Division in Vedic Mathematics / Direct -Flag Method: Shortcut Method to Divide Numbers using Vedic Mathematics

Direct -Flag Method: Shortcut Method to Divide Numbers using Vedic Mathematics

by 31 Comments

 

Vedic Mathematics Flag Method

Flag Method (Direct Division Method )- Division in Vedic Mathematics

Direct Flag Method is a General Method of Vedic Mathematics is used to carry division of ANY types of numbers.

Prerequisites:

In this post you will see  Flag Method Division of Vedic mathematics.  Before starting, It is very important to know Vinculum & playing with Quotients & Remainders.

Examples:

Also Read More Division Sutras in Vedic Mathematics

Flag Method of Vedic Mathematics to divide any numbers

Single Digit Flag

#1. 1234/12 Dividend = 1234 and Divisor = 12. Split divisor (12) in 2 parts (1 and 2) where division will be carried using ONLY 1(new divisor) and 2 is called as flag. As flag is single digit, Split dividend in 2 parts such that 2nd part will have same number as that of flag i.e. 1 digit.

Process (see the example for each step):

  1. Division of 1 by 1 (Q=1 and R= 0). Write Q=1 and carry forward the R=0(written in white under and between 1&2).
  2. Multiply the new Q(1) with the flag(2) and subtract this product from 02 = 0 and divide this subtraction by 1. It gives Q= 0 and R= 0(Carry forward R=0). (i.e. Multiply, Subtract, Divide)
  3. Follow same above process, So multiply new Q(0) with flag(2) and subtract this product from 03 = 3 and divide this subtraction by 1. It gives Q= 3 and R= 0(Carry forward R=0).
  4. For remainder we carry same process EXCEPT we don’t divide. (i.e. Multiply, Subtract) So multiply new Q(3) with flag(2) and subtract this product from 04 = -2. As we get negative subtraction, we reduce the quotient by 1 and increase the remainder by the 1st multiplier of new multiplier (1X1 =1). So new Q = 2 and new R =1. (Refer Topic How to Play with Quotient and Remainder). We carry this method till we don’t have negative subtraction.
  5. Now Multiply the new Q(2) with the flag(2) and subtract this product from 14 = 10(positive) and put it down as it is.
  6. So final answer: Quotient = 102 and Remainder = 10 (Remainder should always < Divisor| (How to Play with Quotient and Remainder).

More Examples: Flag Method of Vedic Mathematics to divide numbers

2-digits Flag

Flag Method of Vedic Mathematics to divide numbers # 15623/123 Dividend = 15623 and Divisor = 123. Split divisor (123) in 2 parts (1 and 23) where division will be carried using ONLY 1(new divisor) and 23 is called as flag. As flag is double digit, Split dividend in 2 parts such that 2nd part will have same digits as that of flag i.e.2 digits.

Rules:

  • We carry out the same process except 1 change. As flag is of 2 digit, whenever we need to do subtraction, we subtract the CROSS multiplication of 2 latest quotient digits with the flag.i.e. if Flag=ab and new Q = cd then subtract (ad+bc).
  • If we have only 1 digit in the Quotient which happens only in starting step then we do multiplication with the 1st digit of flag.
  • It has different way of calculating Remainder. Remainder: Subtract [10(cross multiplication of flag(ab) and latest Q(cd))+ Last digit multiplication of ab and cd i.e. bd]… See examples to get more cleared.

Process (see the example for each step):

  1. Division of 1 by 1 gives Q=1 and R = 0. (Carry Forward R=0).
  2. Multiply the new Q(1) with the 1st part of flag(2)(See above 2nd rule) and subtract this product from 05 = 3 and divide this subtraction by 1. It gives Q= 3 and R= 0(Carry Forward R=0).
  3. Now Cross Multiply (see above 1st Rule) new Q(13) with flag(23) and subtract this product(9) from 06 = -3(negative). Since its negative, reduce the quotient by 1 and and increase the remainder by the 1st multiplier of new multiplier (1X1 =1). So new Q = 2 and new R =1. (See Basic Requisites page).
  4. Cross multiply new Q(12) with flag(23) and subtract the product(7) from 16=9 and divide this by 1 giving Q= 9 and R = 0.
  5. Carry out similar process to get till you reach calculation for Remainder.
  6. Remainder: 223 – [10(6+14) + 21] = 223 – [200 + 21] = 2 (See above 3rd rule).
  7. Final Answer: Quotient: 127 and Remainder: 2.

More Examples on Shortcut Tricks for dividing large numbers in Vedic Mathematics.

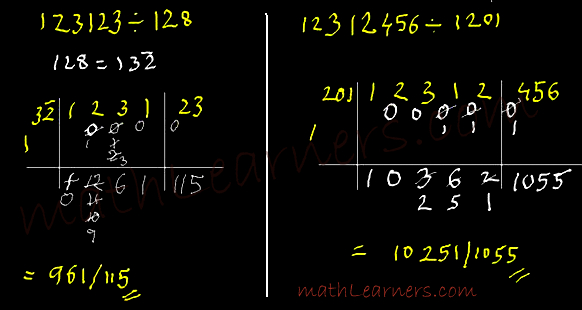
Flag Method of Vedic Mathematics to divide numbers

vedicmathdivisiondirect4-jpg

Answer in Decimal format: We can answer in terms of decimal as well. We append zeroes and carry same process which we used to carry Quotient only difference the step which we had used for calculating remainder will be omitted and even after the vertical line (decimal point) process remains same. Decimal point comes at same place where the Remainder would have come. vedicmathdivisiondirect5-jpg

1452563 / 1234: Remainder part FINALLY will go as 4563 – [100(7×2+7×3+1×4) + 10(3×7+4×7) + 4×7] = 145 (Same problem can be solved by considering flag as 34 and divisor as 12 but for that table of 12 will be required to be known.)

flag-method-_-flag-3digitspng-jpg

What You Think ????

[fb_button]

How the following examples should be solved using Flag Method !!!

1) 473/34 2) 93489/29 3) 783458/112 4) 8274/189 5) 783458/118 6) 1452563/1234 Subscribe us for regular updates

You May Like This to Read As Well ...

How to Divide in 1 line In Vedic mathematics using Ekadhikena Purvena Vedic Mathematics Division TricksShorcuts for Division in Vedic Mathematics Reciprocals Vedic Mathematics Nikhilam SutraNikhilam Sutra – Shorcuts for Division in Vedic Mathematics Vedic Mathematics Nikhilam SutraNikhilam Sutra – Shortcut To Multiply Numbers in Vedic Mathematics

Comments

  1. Dear Sir,

    I may not have done the submission correctly the last time, so pardon me for doing it again.

    Could you tell me where I find the “Proof” of the Flag Method using the conventional arithmetic or algebraic rules?

    Many thanks,

    bill

  2. Dear Sir,

    Could you tell me where can I found the “Proof” of the Flag method using conventional mathematics, like arithmetic or algebra rules?

    Many thanks!

    bill

  3. hello sir,
    sir in dividing 13579 by 1616 I’m not getting when i enter into remainder part.. in (i) part 779 – (16*8) i think.. but sir after entering to remainder section we need to do cross multiplication na sir…
    please guide me

  13. 1. In your 828432/38 example why have you converted the divisor into viniculum number? However, in video you have divided the number 216389 by 48 without conversion.
    2. I didn’t understand how to treat viniculum number in 828432/38 example after step 2.
    Example: 828432/42.
    First digit 2 is fine then howcome we got 2 1 in quotient and 2 as remainder?

    • Hello Rinky,

      1) We can solve the 828432/38 example either by keeping 38 or by converting to Vinculum number.
      If you observe if we use 38, flag will become 8 and multiplication with the flag (8) will everytime result big number. Whereas if 8 is converted to -2 using vinculum then multiplication will result smaller number.
      Hence applying Vinculum helps whenever we have bigger numbers.
      2) 828432/4(bar)2: We apply MSD’s. So 2x-2 = -4, subtracted from 02(So 02 – -4 = 6) and then division 6/4: Quotient =1,Remainder=2.

      Please go through the videos mentioned on the page. This will clear you concepts.

      —
      Rahul

  14. Sir ,

    If suppose we want to divide 1452563/1254 using flag method

    then how to divide 1254 in parts and how to carry out the cross multiplication ….

    Thanks !!

    • Hello Shivam, I have uploaded the problem mentioned by you.

      Steps:
      When only 1 digit is present in Quotient part, multiply that digit with 1st digit of flag.
      When 2 digits are present in Quotient part, CROSS multiply those 2 digit number with 1st 2 digits of Flag
      When 3 digits are present in Quotient part, CROSS multiply those 3 digit number with all 3 digits of flag nummber
      When more than 3 digits are present in Quotient part, CROSS multiply LAST 3 digit number with all 3 digits of flag nummber.

      Let me know if you are clear now.

    • Hi Adarsh,
      you can solve this problem as shown above in 2Digits flag section. You can split Divisor 135 in 2 parts 1 and 35 where 1 will act as ur divisor and 35 as ur flag. If you are confused at particular step let me know where u r stucked.
      OR if you know table of 13 then you can consider 1 digit flag i.e. consider 13 as your divisor and 5 as your flag

    • You need to apply 1 digit flag method. Convert 109 to viculum number and then split and consider 1st 2 numbers as divisor and and last as flag.
      or u can solve without converting to vinculum number as well. In that case 10 will be ur divisor and 9 will be ur flag.

Leave a Reply