Ekadhikena Purvena – Divide numbers in one line.

Shortcut Division when Divisor Ending with 9

Sutra Used:

Ekadhikena Purvena (1 more than the previous)(see more in Squares topic).

Examples:

1/19

I: Method 1 (L –> R):

For the denominator 19, the purva (previous) is 1.
Hence Ekadhikena purva (one more than the previous) is 1 + 1 = 2.
Now we will be using 2 for Division purpose.
Write 1/19 as 1/20 (but remember they are not equal : ))

Steps:

• Divide 1 by 2 which gives Quotient as 0(written with yellow) and Remainder as 1 (written on left side of Quotient with White)
• Now divide 10 by 2 which gives Quotient as 5(written with yellow) and Remainder as 0 (written on left side of Quotient with White)
• Now divide 05 by 2 which gives Quotient as 2(written with yellow) and Remainder as 1 (written on left side of Quotient with White)
• Similarly go on carrying this process till you find same pair of Quotient and Remainder is obtained.
• At the end we get 01, on dividing it by 2 we get Quotient as 0 and Remainder as 1. So that means same series (from blue dot to blue dot) will keep on repeating.
• So the series written in yellow color is final answer.

II: Method 2 (R–> L):

Here as well Ekadhikena Purvena is 2. BUT here we use 2 for multiplication purpose.

Steps: (From R –> L)

• We start by putting 1. Multiply it 2 which gives 2.
• Now Multiply 2 by 2 which gives 4.
• Now Multiply 4 by 2 which gives 8.
• Now Multiply 8 by 2 which gives 16. Carry forward 1 (written in yellow).
• Now multipliy 6 by 2 and add the carry forward to it, gives 13. Carry Forward 1.
• Similarly go on carrying this process till you find same pair of Quotient and Remainder is obtained.
• Finally 0 will be obtained with carry forward 1. Multiplying 0 with 2 and adding carry forward gives 1 which repeats the series.
• So the series written in yellow color is final answer.

III: Method 3 (More Shorter):

Any of the above 2 methods are carried out till a certain criteria and then this method can be applied.
Criteria: Denominator – Numerator (19-1=18). When we get 18(Quotient=8 and Remainder=1) we stop and we go to the other row and in that row we just write the 9’s compliments of above/below digit.
Column wise addition should be 9.

Note:It’s not necessary to get these criteria always. Sometimes we don’t get. So in that case we can stop when series is getting repeated. We will see more about these criteria’s in next topic.

More Examples:

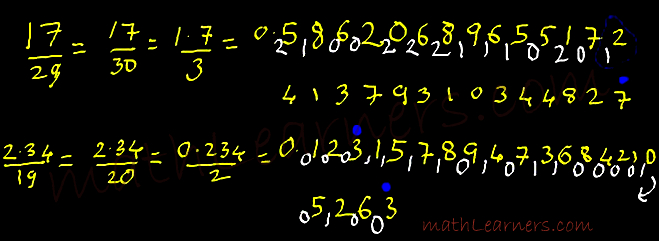
In last Example .234/2 (More than 1 digit after decimal)

• Divide 1st digit(2) by 2, gives Quotient=1 and Remainder=0.
• Add 2nd digit(3) to 01 which gives 4 and then divide by 2. Quotient = 2 and Remainder=0.
• Add 3nd digit(4) to 02 which gives 6 and then divide by 2. Quotient = 3 and Remainder=0.
• Now carry usual method, divide 03 by 2. Quotient = 1 and Remainder=1.

Proof:

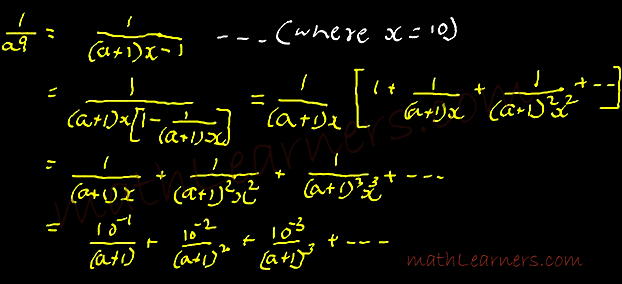
This shows Ekadhikena Purvena (a+1)

Also if a =1 then RHS = 0.1/2 + 0.01/4 + 0.001/8 … (i.e. we divide each previous term by 2).

= 0.05 + 0.0025 +0.000125….

=0.0526….

Anurupyena (Proportionality)

Calculate 7/13.

Multiply and Divide by 3 to have Divisor endiing with 9 and apply above Ekadhikena Purvena Method.

7/13 = 21/39 (HomeWork :))

Divisors ending with 8:

Example: 6/28. Again Ekadhikena Purvena. So 3 is new divisor.

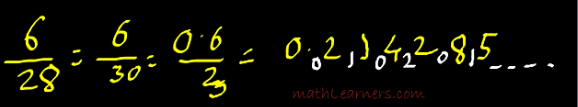
• Divide 6 by 3 which gives Quotient=2 and Remainder = 0
• Now Multiply Quotient (2) with 2(since divisor ends with 8, we double. If divisor ends with 7 then we triple) and divide by 3, gives Quotient=1 and Remainder = 1
• Similarly Multiply Quotient (1) with 2=2 and append the earlier remainder and then divide 12 by 3, gives Quotient=4 and Remainder = 0.
• Similarly carry out this process till some series is repeated.

Divisors ending with 1/2/3/4:

We deduce the numerator by 1.

Divisor ending with1:

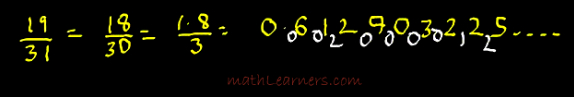
• Divide 1.8 by 3, gives Quotient = 6 and remainder =0.
• Subtract Quotient (6) obtained from 9 = 3(We subtract whenever divisor ends with 1,2,3,4 ), append the remainder 0 and divide by 3, gives Q=1 and remainder=0.
• Similarly Subtract Quotient (1) obtained from 9 = 8, append the earlier remainder 0 and divide by 3, gives Q=2 and remainder=2.
• Similarly Subtract Quotient (2) obtained from 9 = 7, append the earlier remainder 2 and divide by 3, gives Q=9 and remainder=0.
• Similarly carry out this process till some series is repeated.

Similarly for Divisor ending with 3: Only difference we triple the Quotient and then subtract from 9.

Same Process can be followed for any number of digits:

When we have 2 digit divisor, we have Quotient in 2 digits
And we subtract the Quotient from 99(for divisors ending with 1,2,3,4)

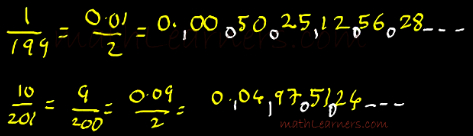
Rules:

• While Appending Remainder(R) with Quotient(Q), R should be present at 10’s digit i.e RQ can be written as 10R + Q.

Eg:

1.  If we have Q = 12 and R as 1 then RQ = 22 (10R + Q = 10×1 + 12).
2. If we have Q = 1 and R as 10 then RQ = 101 (10R + Q = 10×10 + 1).

• After RQ/D, we NEVER want Q > = 10, If we have it so then we need to reduce previous Remainder (R) and thus will be required to increase corresponding Quotient (Q). Watch video and page How to play with Quotients and Remainders.
• Denominator ending with bigger digits like 9, 8, 7, 6: If we have digits in numerator more than that of denominator then we call them as say Extra Digits.
• Denominator ending with smaller digits like 1, 2, 3 ,4: If Numerator > Denominator then we find a number or group of numbers from Numerator and from left side such that it will be lesser BUT closer to Denominator and it will be decremented by 1. Remaining digits from numerator will be called as Extra Digits (say X).Eg:
  1.  12456/23: 12 will form that number which will be decremented by 1 and 456 will be out Extra Digits.
  2. 23768/23: 2 will form that number which will be decremented by 1 and 3768 will be our Extra Digits.
• Denominator ending with Bigger Digits:
• Denominator ending with 9:
  • If Numerator has no extra digits then we use RQ/D
  • If Numerator has extra digits we use [R(Q+X)]/D and when no extra digits are left then we use RQ/D

  Denominator ending with 8:

  • If Numerator has no extra digits then we use R(2Q)/D
  • If Numerator has extra digits we use [R(2Q+X)]/D and when no extra digits are left then we use R(2Q)/D

  Denominator ending with 7:

  • If Numerator has no extra digits then we use R(3Q)/D
  • If Numerator has extra digits we use [R(3Q+X)]/D and when no extra digits are left then we use R(3Q)/D

  Denominator ending with 6:

  • If Numerator has no extra digits then we use R(4Q)/D
  • If Numerator has extra digits we use [R(4Q+X)]/D and when no extra digits are left then we use R(4Q)/D
• Denominator ending with Smaller digits:
• Denominator ending with 1:
  • If numerator is smaller than Denominator use [R(9-Q)]/D
  • If numerator is greater than denominator (i.e. having Extra digits) then use [R((9-Q) + X)]/D and when no extra digits are left use [R(9-Q)]/D.

  Denominator ending with 2:

  • If numerator is smaller than Denominator use [R(9-2Q)]/D
  • If numerator is greater than denominator (i.e. having Extra digits) then use [R((9-2Q )+ X)]/D and when no extra digits are left use [R(9-2Q)]/D.

  Denominator ending with 3:

  • If numerator is smaller than Denominator use [R(9-3Q)]/D
  • If numerator is greater than denominator (i.e. having Extra digits) then use [R((9-3Q) + X)]/D and when no extra digits are left use [R(9-3Q)]/D.

  Denominator ending with 4:

  • If numerator is smaller than Denominator use [R(9-4Q)]/D
  • If numerator is greater than denominator (i.e. having Extra digits) then use [R((9-4Q) + X)]/D and when no extra digits are left use [R(9-4Q)]/D.

You May Like This to Read As Well ...

Ekadhikena Purvena – Trick to Square a number using Vedic Mathematics Shorcuts for Division in Vedic Mathematics Direct -Flag Method: Shortcut Method to Divide Numbers using Vedic Mathematics Reciprocals Nikhilam Sutra – Shorcuts for Division in Vedic Mathematics