Adding and Subtracting Recurring Numbers

 

To know to how to add and subtract recurring numbers we need to know below basics.

• Decimals and the conventions of writing decimals.
• Converting Decimals to Fractions.
• What are Recurring Numbers?
• How to convert Recurring Numbers to Fractions?

 

1) Decimal Numbers:

Decimals Numbers are numbers which are not natural numbers and which always has denominator other than 1.

It’s denoted by a POINT between numbers.

Eg: 1.2, 783.45

• Here, Numbers before decimal (1 & 73) are called Integral Parts.
• 1.2 has ONE decimal place while 783.45 have TWO decimal places.
• 2 and 45 are called as Decimal Values

2)  Converting Decimals to Fractions and writing in terms of powers of 10:

• 1.2 = ¹²⁄₁₀ = 12 x 10^-1 (1 Decimal Place so we moved decimal point  1 place forward and hence needs to multiply by reverse of that many powers of 10 i.e. 10^-1).
• 783.45 = ⁷⁸³⁴⁵⁄₁₀₀  = 78345 x 10^-2 (2 Decimal Places so we moved decimal point 2 places forward and hence needs to multiply by reverse of that many powers of 10 i.e. 10^-2).
• 0.000123 = ¹²³⁄_1000000= 123 x 10^-6 (6 Decimal Places so we moved decimal point 6 places forward and hence needs to multiply by reverse of that many powers of 10 i.e. 10^-6).

 

Standard Form of writing Decimal Number:

When we have very big number or very small number then we follow a standard form for writing decimal numbers. Standard form is to have ONLY ONE digit in Integral Part.

• 0.000123 = 1.23 x 10^-4 (In order to get 1.23 we need to move decimal point 4 places forward. Hence multiply by reverse of that many powers of 10 i.e. 10^-4).
• 987654 = 9.87654 x 10⁵ (In order to get 9.87654 we need to move decimal point 5 places backward. Hence multiply by that many powers of 10 i.e. 10⁵).

 3) Recurring Numbers:

Recurring numbers are decimal number in which decimal values are continuously repeated.

Eg: 1.33333…., 12.45454545…., 65.23678678678….

Representation:

If single decimal value is repeated then it’s represented as a DOT over that number 1.3

If more than 1 decimal value is repeated then it’s represented as a BAR over those numbers 12.45,  65.23678

Types of Recurring Numbers:

• Pure Recurring Numbers
• Mixed Recurring Numbers

Pure Recurring Numbers:

If complete set of Decimal Values are repeated then the recurring numbers are called as Pure Recurring Numbers.

Eg  1.3,  12.45

Mixed Recurring Numbers:

If complete set of Decimal Values are repeated then the recurring numbers are called as Pure Recurring Numbers.

Eg  65.23687, 45.33455

 4) Convert Recurring numbers to Fractions:

Note: Trick is to remove Decimal Values. For this we multiply by powers of 10 as required.

Examples:

2nd example is 17.8 (image got clipped of)

Examples:

Pure Recurring Numbers:

   

Mixed Recurring Numbers: 

   

 

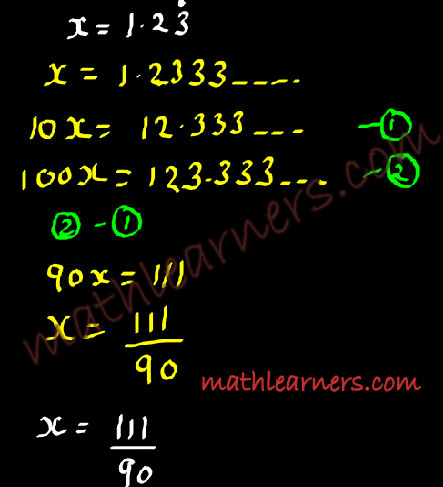
General Forms:

Depending upon the Pure or Mixed Recurring numbers and also the number of digits repeated we can write the General Form to convert Recurring Numbers to Fractions.

Pure Recurring Numbers:

Fraction =

Complete Number (Without Recurrence)- NonRecurring Numbers

Number of 9^’ s as many that of Num.of Recurring Decimal Digits

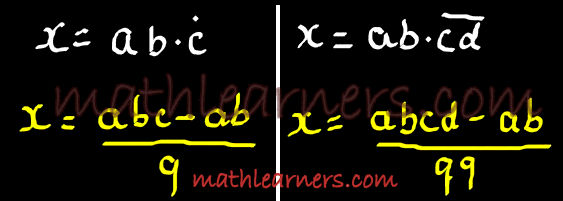
Mixed Recurring Numbers:
Fraction =

Complete Number (Without Recurrence)- NonRecurring Numbers

Number of 9^’ s & 0^’ s as many that of Num.of Recurring & NonRecurring Decimal Digits resp.

 

 5) Adding and Subtracting Recurring Numbers:

Finally coming the original topic  – How to Add and Subtract Recurring Numbers.

Pure Recurring Numbers:

Convert Recurring Numbers to Fractions and then perform Addition or Subtraction.

Examples:

Mixed Recurring Numbers:

To perform Addition or Subtraction we follow below steps:

1. Make 3 compartments.
2. 1st compartment will have Integral Part as well as the Non Recurring Decimal Digits such that number of decimal digits remains same in the compartment so if it requires appending more recurring numbers then do so.
3. 2nd compartment will have Numbers equal to LCM of Number of Recurring digits of both numbers. (In 1st example we have recurring digits as 56 and 235. So LCM = 6).
4. 3rd compartment will have exactly 2 digits.
5. Perform Addition or Subtraction from Right – > Left.
6. Discard the 3rd compartment numbers and rest will be the answer where 2nd compartment numbers will be recurring numbers.

 

Examples: