Paravartya Yogayat (Paravartya)
Division in Vedic Mathematics when Divisor is CLOSER and SLIGHTLY GREATER than power of 10.
Sanskrit Name:
परवर्त्य योजयेत्
English Translation:
Transpose and Apply.
Prerequisites:
In this post I will guide you to shortcut to divide numbers using Paravartya Sutra. But before starting with Paravartya Sutra of Vedic Mathematics, below basic concepts are required.
Vinculum & Concept of Playing with Quotients and Remainders
Specific Condition Required:
Lets see the what Paravartya Division Tricks are required in this Sutra.
- We apply this method when the Divisor is greater than power of 10 (10,100,1000, etc) and starts with 1.
(The Divisor Need NOT to be JUST GREATER than power of 10 since large digits(6,7,8,9) can be converted to smaller digits(1,2,3,4) using Vinculum. Also if Divisor starts with other than 1 then we can apply Anurupyena Sutra. (see in Anurupyena & Vinculum)) - As the name (Transpose and Apply) suggests we change the sign and apply the changed number. i.e. Addition will be turned to Subtraction , Division will be changed to Multiplication and vice versas.
- Remainder Theorem and Horner’s process of Synthetic Division are small parts of Paravartya Sutra.
Also Check => More Division Sutras in Vedic Mathematics
Examples:
- Discard the 1st digit(1) of Divisor(11) and take Transpose of remaining digits(i.e. -1 or Bar 1).
- Split Dividend in 2 parts (Quotient & Divisor) in such a way that Remainder part should have same number of digits thus obtained in 1st step.Thus remainder part will have only 1 digit
- Now carry the same process as done with previous (Nikhilam) method.
- If any bar digit is present in final answer, convert to Normal method using Vinculum.
As seen instead of dividing we multiply and 11’s 1 is turned to -1 (i.e Transpose and Apply).
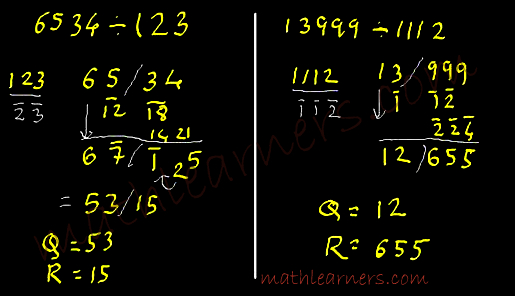

As seen from last example (1356/182), using same above method we had to multiply by 8(bigger number), hence we can convert this bigger digit in smaller using Vinculum Division Method.
Here, using Paravartya Yogayat Sutra Division, we obtained answers in terms of Quotient and Remainders, we can obtain answers in decimal format also using the same process discussed in Nikhilam section of Division. HomeWork 
What You Think ????
[fb_button]
How the following examples can be solved using Paravartya Sutra !!!
| 1) 239479/1203 2) 5644/116 3) 6348/178 4) 34565/128 |
Subscribe us for regular updates
|

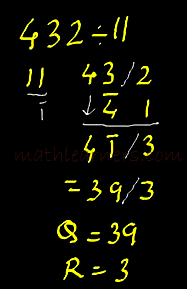




Hello ji 9378 ko 6 se divied kese karenge please solved this problem
how to divide 1487 by 14 Paravartya Yojayet?
I need some examples for division using paravartya for binary numbers.I am not getting correct answer whenever carry occurs pls help me
Dividend 3216 and divisor 14 solve it through paravartya?
72450 div by 125
Pls solve example 239479/1203 by paravartya method???
I am facing problems in this example.
What place you are stuck?
Hi Rahul:
Thanks for your reply. One quick question:
If you end up with a negative number in a column, like, for examole, -123, is that entire number to be considered a vinculum number?, like -1, -2, -3?
Thanks in advance.
Bob Coppedge.
Hello Bob,
If In SINGLE column if it comes -123 then yes whole number is negative But it would be wrong to split single number as -1,-2,-3.
Let me know problem you have came across. It it would easier to check.
Hi Rahul:
I need your help again. I have the Tirthaji book. In my edition, I’m on page 227. He is introducing “Straight Division.” The problem is 38982/73. He first shows this solved by both Nikhilam and Paravartya methods. I figured out the Nikhilam method, but I need help with the Paravartya method,
In case your edition differs from mine, I’m going to try to reproduce mine here.
He starts with:
73
__
1-3 3
______
3 -3
I understand this. He’s using Vinculum to get the first number at 1. Then, reversing the sign.
Then:
3 8 9 | 8 2
9 -9 |
51 | -51
| 153 -153
___________________________________ Answer should be
534 remainder 0.
3 17 51 | 23 949
_____________________________________
534 0 0
I can follow the procedure, but I can’t figure how he arrives at 949 and 23 in the remainder section.
If my figuring is correct, in the quotient section, this would reduce to 521. There would need to be 13 added to this to get the answer of 534. 73(the divisor) times 13 does equal 949.
What am I not seeing in the remainder section? I just can’t figure how he gets 23 and 949 there. Could you please walk me through this?
Thanks in advance.
Bob Coppedge.
Hi Bob,
I checked in the book. Even I am not sure how it was written as 23 and 949… Probably 23 and 949 might not be present in the columns as shown, we come across 949 while solving… or it must be typo error while printing or might have missed some steps in between or some other reason … but anyways your approach is correct and answer should be Q/R as 534/0.:)
–Rahul
1 2 3 7 2 3 6
-2-3
-14 -21
24 36
7 (-12)/ 642
i got this now further??????
pls help me…….
Hello Dhwani,
Similar problem I have solved. Check example: 6534/123
You get answer: Q = 58 & R = 102
ya bt i cnt do it in reminder portion i got 102 bt in quotient portion i cnt get 58????pls help me….
In Quotient part, you got 7(bar)1(bar)2… So this (bar)1 with get carry forwaded to 7. So now you have 6(bar)2.
Now convert this vinculum number to normal number and you will get 58.
For above conversion concept follow this page:
http://mathlearners.com/vedic-mathematics/basic-requisites/
5644 ÷ 116
1 1 6 5 6 / 4 4
-1-6
-5 -30
-1 -6
5 1 / ( -272)
now further???/
pls solve this division by paravartya method
7236 / 123
when i divide using paravartya method 239479 by 1203 and change into decimal
i got 201.(-195446) now wat i do?
how would i deal with 0.195446?
thanks in adavance?
Hi Amit,
Please go through Basic Requisites page
http://mathlearners.com/vedic-mathematics/basic-requisites/
This are requisites understand Vedic Mathematics.
I am sure your concepts will be get solved after going through this.
—
Rahul
I read basic requisites page
when i divide 239479 by 1203 using paravartya method and change into decimal i got Q=201 decimal part =(-195446). u told in playing with remainder video that how to deal with remainder part not decimal .
how i change this negative decimal part to positive decimal part.
pls pls pls tell its very important for my bank exam.
Since the dividend is having bigger digits like 9,7,9 you must have observed difficulty in multiplication and addition and hence it is recommended to convert Dividend to Vinculum number which will have all digits <=5. Also as you are preparing for some competitive exam not much time can be wasted using the method you are trying. Convert to Vinculum and try.
To divide 239479 by 1203 with an answer in a decimal let’s (just to make up an example) say we need the result to two decimal places. Write the divisor as 2 3 9 4 7 9 0 0/ 0 0 0
This represents writing the divisor as 239479.00 and then the three extra zeros to complete the division to the two decimal places and calculate the remainder. Perform the division as written and then recognize where the decimal point goes.
One additional point: if the remainder calculated at the end is more than half of (in this case) 1203, don’t forget to round the number in the hundredth place up one.
when i divide 1452563 by 1234 by paravartya method i got 1177.1176688
but the correct ans =1177.1175040
1 4 5 2 / 5 6 3 0 0 0 0
bar(2) bar(3) bar(4)
bar(4) bar(6) bar(8)
4 6 8
8 12 16
bar(22) bar(33) bar(44)
bar(8) bar(12) bar(16)
44 66 88
24 36 48
1 2 bar( 2) bar(4)/ 11 4 bar(22) bar(12) 74 124 48
1 1 7 6 / 11 2 bar(3) 6 6 8 8
11 77.1176688
tell me where i went wrong?
Sir when we convert any vinculam number to normal number. We take it 10s complement and then decrease the previous number by one.
Thus 1356÷182 using paravrtya method I get -82 which I want to convert in normal number. So I get 13 but there is no previous number in -82 to decrease. I m getting confused where I am getting wrong.?
I am not sure how you got 13.
But this video will help you to clear the concept when 1st digit of a number is a Vinculum Digit.
https://www.youtube.com/watch?v=FV-6qJ2h0NM
how to apply this method in binomial equation
You can check out my polynomials page !!!
http://mathlearners.com/vedic-mathematics/division-in-vedic-mathematics/polynomials/
THANK YOU
how we use this method in binomial equation??????
How to divide 239479 by 1203? Plz help.
Can you let me know where exactly you are stucked ??
239479 will be divided in 2 parts Q(239) & R(479). Divisor after Paravartya would be -2,0,-3. Then apply the method which is provided on this page.
1 2 0 3 2 3 9 4 7 9
-2 0 -3 -4 0 -6
———- 2 0 3
-22 0 -33
———————
2 0 1 /-24 8 4
I have done so far. Since R is negative i took 3 1023′s to the remainder side.
So Q = 198(201-3).
R = (1203*3)-2484=1125.But its not correct.
You seem to have messed somewhere.
You should have got
201 / (bar2)(bar4)8(bar4).
For Remainder: As the 1st digit is itself negative you need to convert entire remainder to negative number and then you will have to take (1203*2) on remainder side.
Watch out this video: http://www.youtube.com/watch?v=FV-6qJ2h0NM&feature=player_embedded
Hope you are clear now …
Let me know if you are not.
ya. its clear now. thank you.:D
Glad to hear that Pamy.:)
Help us to grow by sharing with your friends and follow us on FB.
How to do 239479÷1203?plz help.
Thanks so much for your help. The Remainder was what confused me.
In your example above(432/11), how would you do this if the divisor was 21 instead of 11? If we just bring down the last 1, and making it a -1, how would we adjust if we knew that that the divisor was 21 instead of 11?
Thanks again for your help.
Bob.
You are welcome Bob
Paravartya Sutra can be applied only when 1st digit of Divisor is 1. So if it is 432/21 then You need to apply Anurupyena Sutra (Checkout this link: http://mathlearners.com/vedic-mathematics/division-in-vedic-mathematics/anurupyena-vinculum/).
So if 21 is multiplied by 4 (=84) then Nikhilam can be applied. If 21 is multiplied by 5 (=105) then Paravartya can be applied.
Thanks so much for your video. It clears up many questions.
I can now get some practice problems to work.
I’m having problems with this one:
5644/116
Could you PLEASE guide me through this?
Thanks in advance.
Bob.
Thanks Bob for dropping by.
So the problem 5644/116 can be solved using Paravartya as below:
I am sure by same mentioned method you must have arrived at
Q = 51 and R = -272. (If not then let me know)
Now its required to play with Quotient and Remainder. (I have created a video for this, soon will upload that)
We know that Remainder(R) can never be < 0 and never be >= Divisor. Since R is negative we need to take 3 116’s to remainder side so it will satisfy the condition.
So Q = 48 (51 – 3).
R = 76 (3×116 – 272).
I hope I am clear.
Regards,
Rahul
You can watch video ‘How to play with Quotients and Remainder’ at
http://www.youtube.com/watch?v=KDWoT-ypsfU