Romans

Invasion of Greek civilization by Romans gave rise to Roman Empire. Roman Empire started invasion over Greeks around in 300 BC and gaining complete invasion over them around in 100 AD.

But Romans were not as good as Greek in geometry so they did not had much contributions in geometry. Also Romans used mathematics just for practical purposes like trade, division of land, creating buildings, etc and also due to the cumbersome nature of Roman numerals they could not go much beyond the simple arithmetics which was also not easy to learn.

Roman Numerals are used even today especially were large numbers are not required like on clocks, writing page numbers in the book before the index page, etc.

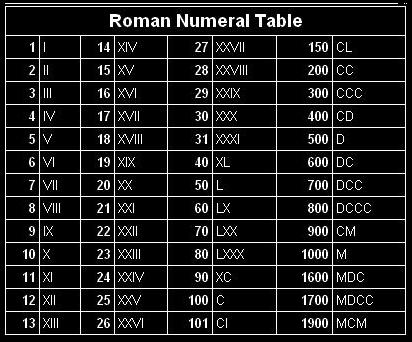
Initially like 1-3; 4 was written as IIII and 9 was written as VIII. But later 4 was written as IV which means (V-I) and similarly 9 was written as IX (X-I) and I in such numbers is called as subtractive prefix. It comes very handy when we have very big and repetitive numbers.

Example 1947:
1000 + 900 + 40 + 7 = 1000 + 500 + 4(100) + 4(10) + 7
= MDCCCCXXXXVII = MDCDXLVII (CCCC= 400 = 500-100 = CD. Similarly XXXX=XL)
= MCMXCVII (DCD = 500+400= 900= M-C = CM)

Roman Addition

Rules:

1. Convert subtractive prefixes to normal (Eg: IV = IIII; IX = VIIII).
2. Concatenate both the numbers (in descending order).
3. Do normal sums like (IIIII = V but don’t write IIII=IV; VV = X)
4. Final answer should be in subtractive prefixes if required.
   (Final answer should not have VIIII, convert to IX)

Example:

106 + 94
= CVI + XCIV
= CVI + LXXXXIIII (Rule 1)
= CLXXXXVIIIII (Rule 2)
= CLXXXXVV (Rule 3)
= CLXXXXX (Rule 3)
= CLL (Rule 3)
= CC (Rule 3)
=200

Roman Subtraction

Rules:

1. Convert subtractive prefixes to normal (Eg: IV = IIII; IX = VIIII).
2. Remove common symbols (VIII- IIII = VI – I).
3. No number should be present after – sign, else keep writing number present before – sign normally (CXXX – VII; Expand one X and remove common symbols, if still number is present after – then repeat it else stop).
4. Final answer should be in subtractive prefixes if required.

Example:

203 – 94
=CCIII – XCIV
= CCIII – LXXXXIIII (Rule 1).
= CC – LXXXXI (Rule 2)
= CLXXXXX – LXXXXI (Rule 3)
= CX – I (Rule 2)
= CVIIIII – I (Rule 3)
= CVIIII (Rule 2)
= CIX (Rule 4)

It’s clearly visible that addition and subtraction even with very small numbers is not as simple compared to that of Hindu/Hindu-Arabic numerals. Roman were also able to do multiplication and division but they were more complex in nature than these.

Romans did not believe in doing arithmetics for trade on piece of paper, instead they invented Abascus which is a portable instrument which can help in simple arithmetic like addition and Subtraction. Abascus was carried and used by everyone like fruits sellers, traders, merchants, engineers, etc.

Abascus, today as well, is used in many parts of world. In China Abascus is used in schools for quick addition and subtraction.

Romans carried such arithmetic almost till 1000 AD till the Fibonacci, Italian mathematician, introduced the Hindu/Hindu-Arabic numerals.

You May Like This to Read As Well ...

Hindu Numerals goes West 400 AD – 1200 AD Basic Requisites – Basics of Vedic Mathematics 1500 BC – 400 AD Post Vedic Period