Ekanyunena Purvena
Shorcut method of multiplication in when multiplier has all digits as 9.
Sanskrit Name:
एकयुनेन पुर्वेन्
English Translation:
By one less than the previous.
Condition:
Ekanyunena Purvena of Vedic Mathematics is applicable whenever the multiplier completely consists of nines.
Either Multiplicand or multiplier should be entirely consisting of 9’s. But for simplicity we will call number with all 9’s as multiplier.
Also Read => More Vedic Mathematics Sutras for Multiplication.
Ekanyunena Purvena Sutra Multiplication has below 3 cases:
I: Case 1:
Digits of multiplicand and multiplier (number with 9’s) are same.
Columns of answer:
- 1st column: 1 less of multiplicand
- 2nd column: complement of above column or (Multiplier – previous column).
II: Case 2:
Multiplier (number with 9’s) has digits less than multiplicand.
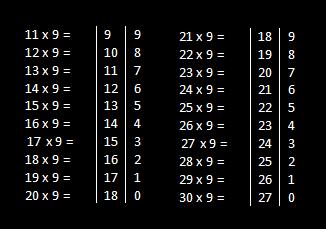
Columns of answer:
- 1st Column: If multiplicand starts with 1, subtract 2 from it.If multiplicand starts with 2, subtract 3 from it and so on.
- 2nd Column: Take compliment of last digit of multiplicand.
III: Case 3:
Multiplier (number with 9’s) has digits more than multiplicand.
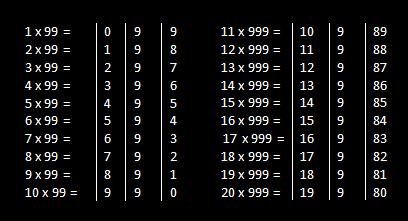
Columns of answer:
- 1st Column: 1 less than Multiplicand
- 2nd column: all 9’s
- 3rd Column: 10’s compliment of multiplicand or (9’s complement of 1st columns). column: all 9’s
You May Like This to Read As Well ...
Direct -Flag Method: Shortcut Method to Divide Numbers using Vedic Mathematics
Nikhilam Sutra – Shortcut To Multiply Numbers in Vedic Mathematics
How to Divide in 1 line In Vedic mathematics using Ekadhikena Purvena
Ekadhikena Purvena – Trick to Square a number using Vedic Mathematics
Antyaordasake’pi – Trick for Multiplication in Vedic Mathematics
Sir will you please tell 345*9
Hi , I tried solving this ,
used 1st two digits of multiplicand (34) and took a number greater than it (i.e 35)
2nd step would be subtracting 35 from 345 that gives 310 (1st part of answer)
for the 2nd part of answer (subtract the last digit of 345 from 10) , that gives 5
combining both gives final answer 3105
with larger numbers I think we can pair the numbers while leaving out the last digit here which can be used to subtract from 10.
Can you please explain 2999*99
Sir please answer this question
here there is another method for this solution.
for example i want to multiply 99*23 than i can write it as (100-1)*23 = 2300-23 = 2277.
another example 26*9 = 26*(10-1) = 260-26 = 234.
The condition does not apply to all. Hence it is said that if multiplicand starts with 2 subtract 3 & take the complement of last digit.
20×9
we have to subtract 3 from 20 =17
And 7s complement is 3
Thus we get 173. But the answer is 180.
Where do I getting wrong.?
Hello Yasmin,
In case of 20 x 9
1st Column: As multiplicand starts with 2, subtract 3 from it. SO, it comes as 17.
2nd Column: Take 10’s compliment of last digit of multiplicand (20). i.e. 0. So it comes as 10
So from 2nd column 1 will get carry forwarded to 1st column making 17+1 = 18 and 0 in 2nd column.
Let me know if I am clear.