HCF using Vedic Mathematics

Finding HCF of expressions using Vedic Mathematics

Highest Common Factor (HCF) as the name suggests it is the highest common factor present between 2 or more expressions or numbers For Example: HCF of 8 and 10 is 2. While that of 8 and 12 is 4 and so on. In this topic we are going to see the HCF of expressions. Calculation of HCF can be done in following ways:

1. Adyamadyena Rule to find the factors of the expression and name the common factor/s as the HCF.
2. Lopanasthapana Method by elimination and retention method or Sankalana-Vyavakalana Process which means addition and subtraction to eliminate and retain the highest power of dependent term.

We will be using 2nd way.

Examples:
Find HCF of x² + 7x + 6 and x² -5x -6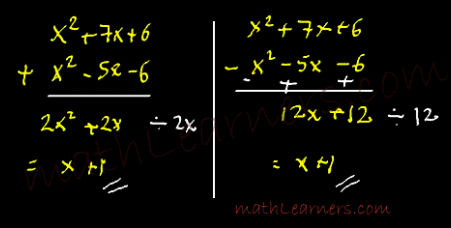

So HCF = x+1

Find HCF of 4x³ + 13x² + 19x + 4 and 2x³ + 5x² + 5x -4
While subtraction we multiplied eq 2 by 2 and done subtracted from eq1 for elimination x³ term.

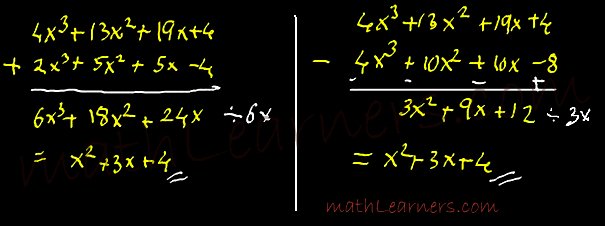
So HCF = x²+ 3x + 4

Find HCF of x⁴+ x³ -5x²– 3x+2 and x⁴-3x³+x²+3x-2

So HCF = x²-x-2

You May Like This to Read As Well ...

Factorization using Vedic Mathematics Solving Equations using Vedic Mathematics Division of Polynomials using Vedic Mathematics Direct -Flag Method: Shortcut Method to Divide Numbers using Vedic Mathematics Anurupyena Sutra – Multiplication in Vedic Mathematics