There won’t be any doubt in saying Egyptians had good knowledge of mathematics just by looking at big monuments like Pyramid of Giza which was built as early as 2650 BC.

Egyptian Civilization

Egyptian civilization was present at the banks of river Nile. Egypt mathematics developed largely from around 3000 BC but could last till only 100 BC. Egyptians used mathematics for their practical purposes. They used fractions on large basis for trade. They also used addition and subtraction for trade but because of their tedious numeral system they had to do multiplication and division with the help of addition and subtraction.

Egyptians used to note their work on papyrus (material which is made from papyrus plant). Because of the fragile nature of papyrus only few of them has survived today.

Egyptians Numerals:

They used Decimal numeral system but without the zero and place value.

They used pictures to denote numerals called as hieroglyphs.

Eg: They used Lotus to denote 1000.

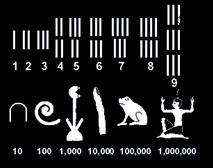
1EgyptianNumerals

2,234 written as

2EgyptianExample
They expressed Fractions as the sum of the DISTINCT UNIT fractions.

Eg: 2/5 was not written as 1/5 + 1/5, instead it was written as 1/3 + 1/15.

Rhind Papyrus

This papyrus was found By Rhind which was developed around BC 1650.It is 536 cm in length and 32 cm in breadth consisted of 84 problems which included various problems on fractions, calculation and usage of pi & Pythagorus theorem , Areas & volumes solid bodies, etc.

Fractions

The fractions 2/n for odd n ranging from 3 to 101 are expressed as sums of unit fractions. For example . The decomposition of 2/n into unit fractions is never more than 4 terms long as in for example . They had their own ways of calculating unit fractions. For eg when denominators were small and prime then they were equated to 2/(p+1) + 2/[p(p+1)].

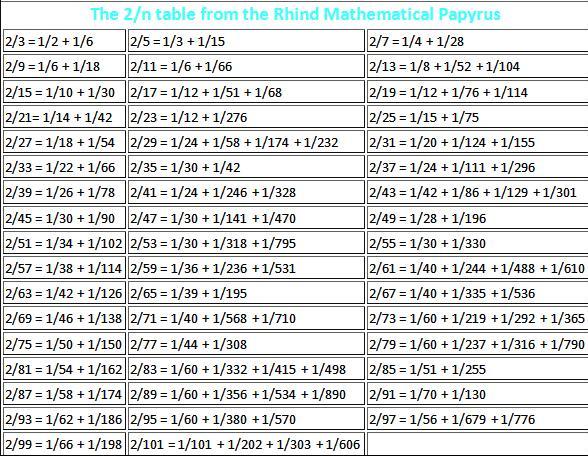
3EgyptianExample
All Egyptian fractions were the sum of distinct unit fractions, such as 43/48= 1/2 + 1/3 + 1/16.

Value of Pi

They took a circle of diameter 9 and inscribed that in a square. So each side of square becomes 9. Each side was trisected and the corner triangles where removed.

So the Area of that octagonal figure approx becomes Area of big Square– 4 x Area of removed triangles.

So, 92 – 4 x [1/2 x 3²] = 63 = 64 (approx.)

Area of circle = A=π((9/2))² = 64

Thus π = 256/81 = 3.16

Areas & Volumes

Some problems calculated the volume of cylindrical and rectangular based granaries and also calculated and used pi as 3.16.

Thus for them Area of circle = (16/9)²r².

Volume of cylinder = (16/9)²r²h.

Pythagoras Theorem

Some believe that they knew Pytharorus theorem as they were able to built pyramids which followed concepts of slopes (Hypotenuse) and the angles. (Pythagorus theorem is attributed to Greek mathematician Pythagorus who was born almost 1000 years later)
But there is no exact evidence to show that they were aware about the Pythagorus theorem. But Rhind papyrus has concept of 3-4-5 triangles (9+16=25) which was used to construct perfect right angles triangles shows that they might have some idea about Pythagorus theorem.