mathlearners

You are here: Home / What is Vedic Mathematics / Shorcuts for Division in Vedic Mathematics / Nikhilam Sutra – Shorcuts for Division in Vedic Mathematics

Nikhilam Sutra – Shorcuts for Division in Vedic Mathematics

by 45 Comments

 

Vedic Mathematics Nikhilam Sutra

Nikhilam Sutra Division – All from 9 and last from 10

Division using Vedic Mathematics when Divisor is CLOSER and SLIGHTLY SMALLER than power of 10.

Stuff you need to know before starting:

In this post I will guide you through the vedic maths division by nikhilam method. But before starting with shortcut to divide numbers using Nikhilam Sutra, you need to go through the concepts of Vinculum, How to play with Quotients and Remainders and Nikhilam Sutra.

Examples:

# 12/9.(See Below)

  1. 9 is 1(deficiency) less than 10(nearest power of 10). (that 1 is written in white color below divisor in below example)
  2. Split Dividend in 2 parts (Quotient & Remainder) in such a way Remainder to
    have same number of digits as that of Divisor. In this case its 1 digit.
  3. Take 1st digit – 1 down as it is.
  4. Multiply the above deficiency (1) with the 1 and put
    below 2 and add them column wise.
  5. Thus Quotient=1 & Remainder=3.

 

# 3483/99.(See Below)

  1. 99 is 01(deficiency) less than 100(nearest power of 10). (Concept of Nikhilam – All from 9 and last from 10)
  2. Split Dividend in 2 parts (Quotient & Remainder) in such a way Remainder to have same number of digits as that of Divisor. In this case its 2 digits.
  3. Take 1st digit – 3 down as it is .
  4. Multiply the above deficiency (01) with the 3 and put them below 4 and 8(as shown), add 1st column (4+0=4).
  5. Multiply the above deficiency (01) with the 4 now and put in next columns (as shown), add 1st column (8+3+0=11).
  6. In General, Repeat this process till a number comes in last column. In this example a number (4) has appeared in last column so stop here and add columnwise.
  7. Q = 34 and R = 117. But we know concept that Remainder can NEVER be >= Divisor. As R(117) > D(99) Apply ‘Method of How to play with Quotients and Remainders‘ i.e. Divide 117 by 99 gives Sub-Quotient = 1 and Sub-Remainder = 18. Add Sub-Quotient(1) with original Quotient (34) = 35 and now sub-Remainder becomes our Final Remainder.
  8. Thus Quotient=35 & Remainder=18.

Also Read => More Division Sutras in Vedic Mathematics

Similarly apply same process for rest of the examples.

VedicMathematicsDivisionNikhilam1
VedicMathematicsDivisionNikhilam2

VedicMathematicsDivisionNikhilam3

Again…Vinculum can be applied whenever we have bigger digits in either Quotient or Remainder.
In above example we had 172…We can convert it to Vinculum for more simplication.

Lets see similar problem in which we can convert to Vinculum and then apply Nikhilam.
Eg: 167388/87 = ? … (As Quotient is having bigger digits convert it to Vinculum Number).

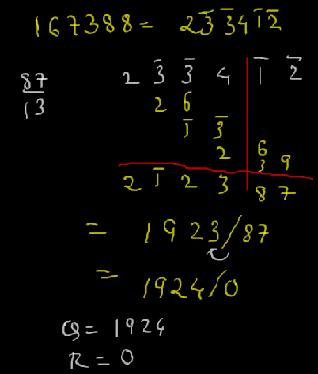
nikhilam_vinculum-jpg
 

Nikhilam Division Tips:

  1. Do not fail to consider 0/0’s after subtraction in initial case of Divisor. (1000-996 = 004)
  2. We can convert the deficiency to Vinculum Number for simplicity. For above example divisor 828 is 172 less than 1000, so we had to multiply by 7’s. You can convert 172 to vinculum number i.e. 2(bar3)2 and then apply Nikhilam to avoid multiplication with 7’s.

 

In above examples we obtained answers in terms of Quotient and Remainders. But if we need answers in form of Decimal still we can apply same Sutra.

# 3483/99 (same above example but in terms of Decimal Point)

  • Split Dividend in 2 parts in such a way later part to have same digits as that of Divisor. In this case its 2 digits.
  • Append Zeroes’s at end of dividend as shown below.
  • Now apply same discussed process .Only stop when you feel stopping or till required number of digits after decimal point.
  • In previous examples, if Remainder obtained >= Divisor then we divide and carry forward thus obtained quotient and add with the quotient obtained earlier and New remainder becomes actual remainder. But since in this process we have answer in terms of decimal, we just carry forward if any carry forward present. Hence we carry forwarded 1 as it is to add with 34.
  • Decimal point will come at same place from where Remainder would have started.
  • Final Answer: 35.1818(till 4 digits)

VedicMathematicsDivisionNikhilam4

Similarly find answer for above examples in decimal form (HomeWork :))

What You Think ????

[fb_button]

How the following examples can be solved using Nikhilam Sutra !!!

1) 2345 / 97
2) 873457 / 972
3) 3523 / 922		 Subscribe us for regular updates

You May Like This to Read As Well ...

Vedic Mathematics Division TricksShorcuts for Division in Vedic Mathematics Vedic Mathematics Paravartya SutraParavartya – Division using Vedic Mathematics Vedic Mathematics Anurupyena SutraHow to divide in Vedic Mathematics using Anurupyena Sutra & Vinculum Vedic Mathematics Nikhilam SutraNikhilam Sutra – Shortcut To Multiply Numbers in Vedic Mathematics Basic Requisites – Basics of Vedic Mathematics

Comments

  1. Please answer this asap-12th boards i need it.
    divide 31 by 8,in decimal format.
    I want 3 digits accurate.
    I am getting 3.716 repeatedly(10 times+)-the answer is supposed to be 3.875
    Anyway please just show the solution as a whole.
    Please.

  4. how can we divide 97 by 13?? However tried i am getting Q=7 and R=0. but we know that it’s not the right solution. Can you kindly help me with this??

  5. 222221/619 1000-619=381
    222|221
    76 2
    3 429
    ————-
    2911|8410
    301|850

    bt actual ans is 359|000
    what is the actual process to get right ans?? help

    • Hello Harikrishna,

      Let me know how many zeroes you had appended to dividend.

      And Yes, if you need to get answer in decimals, more exact answer, you need to append more and more Zeroes to Dividend.
      As you must have observed more zeroes you append more carryforwards you obtain and that gives more accurate answer.

  9. Hello Sir, i hv a problem 12834 divided by 89 in which i am stuck at 3rd digit 8 as follows :
    89 128 | 34
    11 11
    3 3

    —————
    13(12)
    at 3rd digit my sum is 8+1+3 =12 . can you plz tell me how to proceed next as i am not able to get correct answer if i follow the regular nikhilam process

  10. Hi Rahul..i was trying to use this Nikhilam method to solve 28961/99 upto 5 decimals. But i’m getting the answer wrong. Please help me in this regard. Can you solve this for me and explain the same.

    Thanks,
    Suresh.

      • Hi Rahul..i made a silly mistake in Nikhilam method and now i solved it myself. I regret for the inconvenience caused to you.

        But, now while practicing Ekadhikena sutra for division i’m getting a problem, this time i checked it multiple times but i’m unable to solve the problem. Let me explain you what i did.

        234891/39 = ?

        now,

        23489.1/4

        then by doing 23/4 we get
        => R3 Q5

        Next adding 5 with 4 i.e., 5+4=9, appending 3 to it becomes 39 => 39/4.
        => R3 Q9

        Next adding 9 with 8 i.e., 9+8=17, here Remainder 3 is added to ‘1’(in 17) so now it becomes 47 which leaves 11 as quotient when divided by 4, which should not happen. Hence, Remainder 3 should be reduced and Quotient should be increased. Since, Q is 9 & by incrementing it becomes 10 and in this ‘1’ is added to previous quotient ‘5’ which becomes ‘6’. And R 3 is subtracted from divisor 4 hence it becomes ‘-1’ if i’m not wrong. Therefore the new quotients become like this
        -> R3Q6 R-1Q0.

        Now this ‘0’ is added to ‘8’(from dividend) => 0+8=8 then 8 is appended by ‘-1’. so,
        8
        -1
        =>7 =>7/4 gives Q as 1 and R as 3.

        The new answer becomes like this R3Q6 R-1Q0 R3Q1.
        Now, Q1+9(from dividend) = 10 and to this R3 is added, so now it becomes 40 which should be divided by 4 and again it is not possible. So, increment Q1 by 1 and subtract R3 by Divisor 4. The new result becomes => R3Q6 R-1Q0 R-1Q2.

        Now, Adding 2+9 = 11 and then 11
        -1 => 01 => 01/4 = R1 Q0
        The new result R3Q6 R-1Q0 R-1Q2 R1Q0.

        Again, 0+1(from dividend) = 1 which is appended by 1 gives 11,
        11/4 = R3 Q2 => R3Q6 R-1Q0 R-1Q2 R1Q0 R3Q2.

        Now onwards calculations are easy 32/4 = R0 Q8,then
        8/4 = R0 Q2,then 2/4 = R2 Q0 and so on…

        The final result becomes like this
        23489.1/4 = R3Q6 R-1Q0 R-1Q2 R1Q0 R3Q2 R0Q8 R0Q2 R2Q0…..
        23489.1/4 = 6020.28205…but the actual answer is
        234891/39 = 6022.846153…

        I really don’t know where i went wrong. Please Rahul help me in this regard i’m really trying very hard to learn Vedic methods to perform Divisions which is very helpful for my exams. And also please tell me how to put the decimal after the answer is found out, i’m not clearly getting how to observe and where to put the decimal.

        Thanks,
        Suresh.

          • Thank you for giving reply Rahul..I already saw all your videos, with the assistance of those clips only i tried to solve some problems and then i got stuck in this one…i tried many times but i’m unable to find where i went wrong. I have given each and every step of what i’ve done, please guide me where i went wrong (as i’ve checked it multiple times but couldn’t find the mistake).

            Thanks,
            Suresh.

          • Hello Suresh,

            You seem to have messed up in 1st step itself.
            “Therefore the new quotients become like this
            -> R3Q6 R-1Q0.”

            Your thoughts were correct that when you got 3539 the Quotient needs to be increased but increasing 9 gives 2 digit number we need to go 1 more step back i.e. from start.

            So for 35, we need to increase Q (5) by 1 same time Quotient needs to decremented by 1. Then we get -16…

            So final answer is -16000232.182406211533

            Let me know if this is clear. Also if you you more queries on Ekadhikena Purvena, Please post in topic’s content

  12. I am having problem to find answers in decimals. When I dont have to take carry forwards I am able to solve the sum. But when I have to take carryforwards my aanswers are always getting wrong. Will you plz help me out. Or tell me which video should I watchoto clear this concept. Thanks for giving your precious time.

  14. Again, thanks so much for your help.
    Recently, I had to divide 258 by 12. The answer is 21 and a half. I decided to try this using the Nikhilam method both with the quotient as it is, and also in Vinculum form.
    I multiplied the divisor(12) by 8 to get 96. This would result in 04 to work with. So I put:

    04 2 58

    I brought down 2 as it is and continued, and so on. I end up with:

    2 58
    08

    2 5 16

    This comes to a quotient of 2 and a remainder of 66. I multiply 2 by 8 and get 16. Since the remainder is 66, this works out perfectly. Adding 5 to 16 gives 21, and the remaining 6 is 6/12, or one half.

    My problem is when I tried this using the Vinculum form.
    I think that the Vinculum for 258 is 3,bar4, bar2.
    So, everything is the same process as above. Now it is:

    04 3 -4 -2

    I bring the 3 down as it is . Then:

    3 -4 -2

    0 12

    -4 10

    I multiply 3 times 8 and get 24. I know that this has to come down by 3, so the remainder should be a negative 42, so that the 3 times 12 would be 36 and would leave 6 which would make it correct.

    Could you please tell me what I’m overlooking here? It’s probably something very simple.

    Thanks in advance for your help.

    Bob.

    • Hello Bob,

      You went wrong on very last step.

      In Remainder section, bar4 10 will give bar3 0 (1 carry forwards). which is nothing but -30.

      Since divisor is 12 and to make remainder as +ve, 3 12’s need to be transferred from Quotient to Remainder secttion.

      So R will become 12×3 – 30= 6
      and Quotient becomes as 24-3 = 21.

  15. Thanks so much for your help. I just want to check out a problem with you to see if I’ve done it right. I used for practice 87×1924, which is 167388. So I knew that if 167388 was divided by 87, the quotient should be 1924 exactly.
    So, I made a grid, something like the one you showed me above.
    So, 87 from 100 is 13. Doing the process, and, keeping the quotient and remainder separate, after shifting the quotient, I come up with 1911. In the remainder, under the first 8, the total is 100. Under the second 8, the total is 131. I was puzzled as how to handle this. Then , I realized that IF I shifted the “13” from the 131 to the left, the box under the first 8 would be “113.” This, then, would make the remainder 1131. This being the case, everything works out, since 1131 is higher than the divisor(87), the divisor goes into 1131 exactly 13 times. Adding the 13 to 1911 brings it to 1924, which is the correct answer.

    Have I done this right? I hope so.

    Thanks again for your help.

    Bob Coppedge.

  16. i am new to vedic maths. ur website is really gr8. just wanted to know if the divisor is equal to 800 or more we can use nikhilam method for directly without changing into vinculum method right? but if the divisior is like 683 then how we will change to vinculum number and use nikhilam maethod. can u post few more videos on this type. ur videos are really great..one last thing i solved 2345/97, 873457/972 and 3523/922 answers are Q=23 and R = 51, Q = 875 R= 893, Q=37 R= 57 but answer with calculator is showing variance. why so….looking forward for the new video on nikhilam with divisor around 678, 567, 765 etc. Thanks

  17. Thanks so much for your help. After watching your video on remainders, I did get the problem 2119/29 to work out to 731 EXACTLY. Thanks again for your help.

    I hope you will do more videos soon.

    Bob.

  18. Thanks so much for your help. I’ve been working on another problem. I just did it over again, and I think I’ve almost got it, but not quite. The problem is 2119/29. I know that the answer is 731 even. So, I use the method as in the previous problem. 211 for the quotient and 99 for the remainder. Again I multiply 29 by 3 and get 87. This leaves, as before, 13.
    So, I bring down 2 as it is. I multiply 1 and 3 by 2 and put 2 and 6 under each 1. 1+2 gives 3. I bring that down and multiply 1 and 3 by 3 and put 3 and 9 under the 1 and 9. I add 1, 6, and 3 and get 10. I multiply this by 1 and 3 and get 10 and 30. These go under the last two 9s. Adding all this up, I get 2 3 10 28 39. Going across with this, I come up with 243 and 19 in the remainder. If I multiply 243 by 3, I get 729. How do I get this to 731? Thanks again in advance for your help.

    Bob.

    • Remember 1 thing Quotient and Remainder are 2 different numbers so when you want answer in terms on Quotient and Remainder you CAN NEVER carry forward numbers from R to Q. You need apply principle Remainder can never >= Divisor. Check out my Basic Requisites Page and videos on “How to Play with Quotients and Remainders” from that page.

      However when it comes to finding answer in decimal. Whole number is a single number. So in that case you carry forward numbers from 2nd part to 1st part.

      Did I clear you now ??

  19. Thanks so much for your instructions. My question is how do you handle a situation if you want the quotient to have the remainder in decimals and the remainder is, for example greater than the divisor?
    Example: To divide 1411/29, I first multiplied 29 by 3, giving 87. That gives 13 to use the Nikhilam method. I do get the correct answer 48 with a remainder of 19, but the remainder must be adjusted from 106-87 to 19. How would you get to an answer in decimal remainder? Thanks so much for your help.

    • So Bob, What I got is that you want the answer in terms of decimal after applying Anurupyena (multiplication by 3) and Nikhilam (13 less than 100).

      So

      1 4 1 1 0 0
        1 3
          5 15
          9 27
          25 75
      1 5 9 25 52 75

      = 15.1 2095

      = 16. 2095

      Now as per Anurupyena Sutra multiply COMPLETE NUMBER by the factor used earlier i.e. 3 (29×3=87)

      So Final Ans = 48.6285. (More Accurate answer can be obtained by appending more zeroes.)

      I hope you were looking for same. If not then let me know

    • 723 is 277 less than 1000. So if you apply Nikhilam directly you will have to do multiplication with 7’s So it is recommended to convert 277 to Vinculum number i.e. 3(bar2)(bar3) and then apply Nikhilam.

      So in this case multiplication will be required to be done with 3, -2, -3.

Leave a Reply