Cube Roots in Vedic Mathematics

Cube-Roots

Facts:

1. Cubes from 1- 10

1. Cube roots need be grouped in a group of 3 from R –> L.Thus the number of groups formed will be == Number of digits in the cube root.For example (for perfect cubes).
2. 1728 will be grouped as 1,728. Thus its cube root will be of 2 digits84604519 will be grouped as 84,604,519. Thus its cube root will be of 3 digits.300763 will be grouped as 300,763. Thus its cube root will be of 2 digits.
3. Always the 1st group will decide the 1st digit of cube root.Find the perfect cube which is <= 1st group and its cube root will be 1st digit of given number’s cube root.

For above examples

1. As seen from above table, when we have 2 groups we can directly write the cube root(2 digits) i.e. Calculating cube root of a number having <=6 digits is very simple and doesn’t require more steps. But if we have more than 2 groups we need to use some other logic.
2. 3 digit number(cba) can be written as a+10b+100c. Its cube:(a+10b+100c)³= a³ + 1000b³ + 10,00,000c³ + 30a²b + 300a²c + 300ab² + 30,000ac² + 3,00,000bc² + 30,000b²c + 6000abc.= 10,00,000c³ + 1,00,000 x 3bc² + 10,000 x (3ac²+ 3b²c) + 1000 x (b³+6abc) + 100 x (3a²c + 3ab²) + 10 x 3a²b + a³.
   

   Places	Ten lakh/ 1 million	lakhs	Ten Thousands	Thousands	Hundreds	Tens	Unit
   	c3	3bc2	3ac2+ 3b2c	b3+6abc	3a2c + 3ab2	3a2b	a3

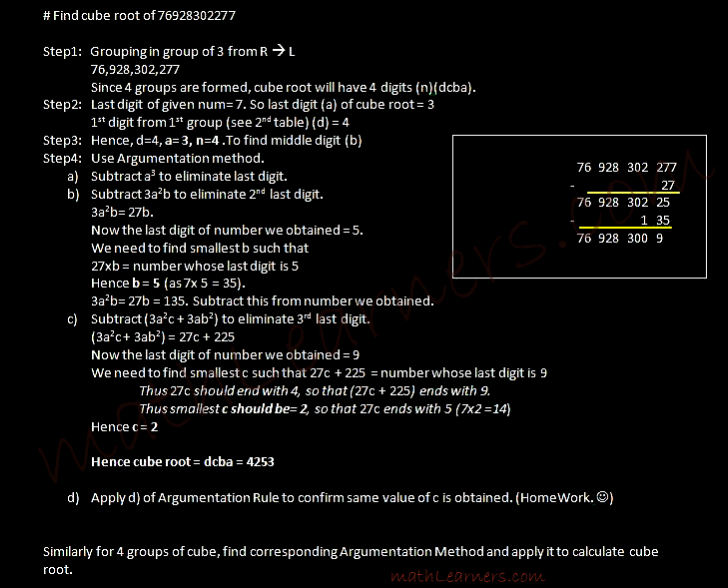
Argumentation Method (Vedic Math Cube Root for a 3 digit number):

It is a method of eliminating process of reasoning methodical.

1. From unit’s place, subtract a³ and this will eliminate last digit.
2. From ten’s place, subtract 3a²b and this will eliminate 2nd last digit.
3. From hundreds place, subtract (3a²c + 3ab²) and this will eliminate 3nd last digit.
4. From Thousands place, subtract (b³+6abc) and this will eliminate 4th last digit and so on.

Examples:

You May Like This to Read As Well ...

Square Roots in Vedic Mathematics #@1 How to find cube of a number using Anurupyena in Vedic Mathematics Cubes In Vedic Mathematics #@2 Yavadunam – To Find Cube in Vedic Mathematics Ekayunena Purvena – Shortcut method to multiply numbers using Vedic Mathematics